



Next: Parallelisierungsansatzdynamische Lastverteilung
Up: Das FE-Programm FLOW
Previous: Das FE-Programm FLOW
Bei der Simulation von Wasserströmungen mit der FE-Methode ist es notwendig, die Wasserspiegeländerungen in Zeitschritten zu betrachten. Zu Beginn der Berechnung ist nur ein Teil des Gebiets benetzt. Die Anzahl der benetzten Elemente eines FE-Netzes ändert sich daher während jedes Rechenschrittes. Grundgedanke der Moving Boundary Method ist, immer nur die zum betrachteten Zeitpunkt benetzten Elemente in der Berechnung zu berücksichtigen. Trockene Elemente werden nicht betrachtet. Ein Element wird als benetzt definiert, wenn in einem Knoten des Elementes die Summe aus initialer Wasserhöhe H und der Wasserspiegeländerung 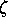 größer ist als ein vorher definierter Wert
größer ist als ein vorher definierter Wert  .
.
Während jedes Rechenschritts wird eine Elementmatrix für jedes Element berechnet. Durch ein Galerkin Lumping dieser Matrix erhält man eine Diagonalmatrix [ULM, 1994]. Das hieraus folgende Gleichungssystem kann für jedes Element getrennt berechnet werden. Die Ergebnisse der Berechnung, Wasserhöhen und Geschwindigkeiten in den Knoten, müssen über die zugehörigen Knoten superponiert werden.
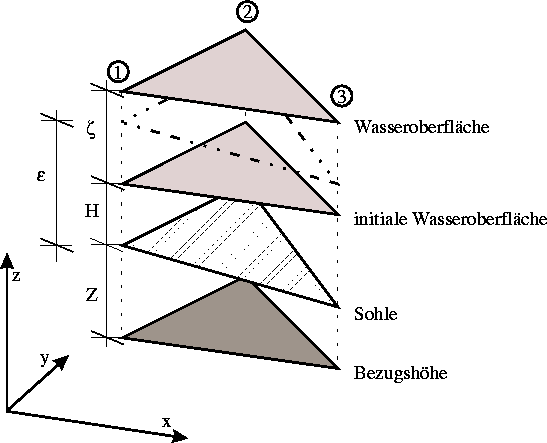
Abbildung: Definition benetztes Element
Als Ansatz der FE-Berechnung wurden folgende Gleichungen verwendet:
1. Massenbilanz
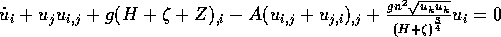
2. Impulsbilanz
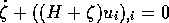
Hierbei bedeutet:¯
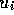 : Geschwindigkeit
: Geschwindigkeit
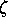 : Wasserhöhe
: Wasserhöhe
H: Anfangswasserhöhe
Z: z-Koordinate der Sohle
g: Erdbeschleunigung
A: Viskosität
n: Reibungsbeiwert
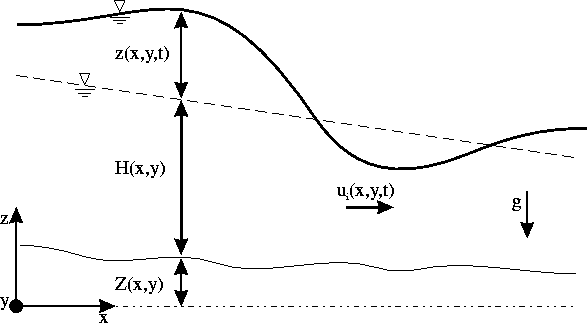
Abbildung: Erläuterung zu den Gleichungen
Die Gleichungen werden nach der Standard-Galerkin-Methode diskretisiert. Hierbei werden als Ansatzfunktion lineare Dreiecke gewählt. Das Programm verwendet eine Zwei-Schritt-Methode zur Lösung der Gleichungen. Der erste Rechenschritt kann wie folgt beschrieben werden:
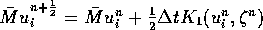
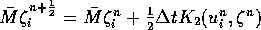
Der zweite Rechenschritt:
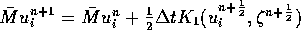
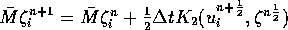
Michael Burghardt





